Kolmannen viikon tehtävät
Tehtävien palautus torstaina 14.11. klo 21:00 mennessä.Tehtäväpohjassa on valmiiksi koodi joka arpoo ensin radiaaneja ja muuntaa sen tämän jälkeen kulmaksi. Kulmaluku voi siis olla yli yhden kierroksen. Tehtävänäsi on kirjoittaa valmiiksi annetun osuuden jälkeen koodi joka kertoo mihin yksikköympyrän neljännekseen arvottu kulma sijoittuu.
Arvottu luku 0.33797175599533125 on alueen (0,1) keskella Arvottu kulma = 337.97175599533125 astetta on 4. neljanneksessa
Arvottu luku 0.09602578231894476 on alueen (0,1) alussa Arvottu kulma = 96.02578231894476 astetta on 2. neljanneksessa
Vaikka Pythonissa on lukuisia kirjastoja, jotka tarjoavat valmiita ratkaisuja ongelmiin, monissa tieteellisen laskennan ongelmissa joudutaan tekemään omia funktioita.
Pythonin funktiorakenne on yksinkertainen:
def funktion_nimi(parametrit):
funktionRakenneTänne
Esimerkiksi funktio joka muuttaa Celsius-asteet Fahrenheiteiksi on seuraavanlainen:
def fahrenheit(TCelsius):
return (TCelsius * 9/5) + 32
Mainissa fahrenheit-funktiota kutsuttaisiin esimerkiksi seuraavasti:
def main():
print(fahrenheit(12))
def fahrenheit(TCelsius):
return (TCelsius * 9/5) + 32
Huomaa, että tehtäväpohjissa nähty main on siis oikeasti myös funktio, joka sisältää pääohjelman!
Funktion rakenne voi sisältää lähes mitä vain. Esimerkiksi for-, while- ja if-rakenteita.
Main-ohjelmarungossa on valmiiksi komento print(factorial(12)). Tehtäväsi on kirjoittaa factorial(n)-funktio, joka laskee annetun luvun n kertoman ja palauttaa sen. Tulosta lopuksi mainissa oleva factorial(12).
479001600
Main-ohjelmarungossa on valmiiksi komento print(exponential(1,100)). Tehtävänäsi on kirjoittaa funktio, joka laskee ex-funktion Taylorin sarjan arvon pisteessä x, n:n termin tarkkuudella. Mainissa oleva funktiokutsu siis tarkoittaa e1 arvoa 100 termin tarkkuudella. Vinkki: käytä edellisessä tehtävässä luomaasi kertomafunktiota. Voit kutsua toista funktiota toisen sisällä aivan kuten kutsuisit sitä mainissakin.
Taylorin sarja lasketaan e^x seuraavasti:
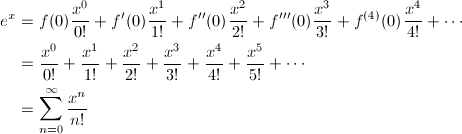
2.7182818284590455
Python3:n float-tyypillä on monia ominaisuuksia. Datan käsittelyssä tahdomme usein vähentää desimaaleja. Tutustu laajaan formatointiohjeeseen täällä.
Seuraavaksi todella yksinkertainen harjoitus Pythonin float numeroiden formatista. Tehtäväpohja on seuraavanlainen:
def main():
a = 2/3
b = np.pi
c = 11.123123123123
Tehtävä on tehty oikein, kun tulostat:
0.67 3.1416 11.123 0.67 3.1416 11.123
Mittauksista ja muista tutkimuksista saadaan usein isoja, jopa tuhansien rivien datatiedostoja. Näiden käsittelyyn Python3 on tehokas työkalu.
Datan käsittely tapahtuu Python3:ssa helpoiten file-tyyppisillä muuttujilla. Ensin määritellään, mitä tiedostoa käsitellään, kuinka sitä käsitellään ja miten käsittely jatkuu. Lopuksi tiedosto suljetaan, jottei se korruptoidu.
def main():
file = open('input.dat', 'r')
Ylläoleva komento avaa tiedoston input.dat ja asettaa sen lukutilaan. Lukutilassa voimme kätevästi siirtää datatiedoston arvoja muuttujiin.
def main():
file = open('input.dat', 'r')
tiedot = file.readlines()
x = []
y = []
for rivi in tiedot:
osarivi = rivi.split()
x.append(float(osarivi[0]))
y.append(float(osarivi[1]))
Ylläoleva koodi siis avaa input.dat-tiedoston ja lukee siitä kaksi saraketta muuttujiin x ja y.
NumPy sisältää myös kätevän tiedoston luku ominaisuuden.
def main():
infile = 'input.dat'
x = np.loadtxt(infile, usecols=(0,))
y = np.loadtxt(infile, usecols=(1,))
Ylläolevalla komennolla käyttäjän ei tarvitse käydä dataa uudelleen for-loopilla läpi vaan se saadaan suoraan muuttujille.
Vastaavasti tiedostoon kirjoittaminen toimii lähes samalla tavalla.
def main():
file = open('output.dat', 'w')
Nyt olemme alustaneet output.dat-tiedoston ja määrittäneet että siihen tallennetaan tietoa. Seuraava vaihe riippuu täysin siitä mitä tiedostoon halutaan laittaa, mutta esimerkiksi lukujen kirjoitus tapahtuisi seuraavasti:
file = open('output.dat', 'w')
i = 0
while (i < len(x)):
file.write("%6.2f\n"%(x[i]))
i++
file.close()
Tämä koodi kirjoittaa kuvitellun muuttujan x listan kokonaisuudessaan output.dat-tiedostoon, siten että luvut ovat allekkain.
Tehtäväpohja on seuraavanlainen:
def main():
lista=[]
#Tee tehtävä tähän
###################################
print(lista)
Tehtävän mukana tulee tiedosto model.dat. Tehtävänäsi löytää datasta rivi, missä on D-sarakkeessa luku 25 (25. päivä) ja siirtää se annettuun lista muuttujaan. Tehtävä on oikein, kun listassa on seuraava rivi:
['2454399.48 2007 10 25 23 35']
Tehtäväpohjassa tulee mukana input.dat-tiedosto. Tehtävänäsi on lukea input.dat-tiedosto ja luoda output.dat-tiedosto, joka on valmiiksi LaTeX-taulukko muotoa. Output.dat-tiedostossa pitää olla yhdellä rivillä 8 lukua ja rivejä pitäisi olla 25. Tehtävä on oikein, kun output.dat-tiedosto näyttää seuraavalta:
0.01 & 7.73 & 1.20 & 7.69 & 2.05 & 7.72 & 3.13 & 7.69 \\ 4.16 & 7.69 & 5.03 & 7.70 & 5.14 & 7.71 & 5.17 & 7.73 \\ ...
Huomaa, että testien läpäisemiseksi rivien tulee olla tarkalleen esimerkin mukaisessa formaatissa (jokaiselle luvulle on varattu kahdeksan merkin tila, luvun jälkeen kaksi välilyöntiä ennen &-merkkiä).
Tehtäväpohjassa tulee mukana input.dat-tiedosto. Tehtävänäsi on lukea tämä tiedosto, jossa on 528 riviä, ja luoda output.dat-tiedosto, joka on valmiiksi LaTeX-taulukon muodossa. Output.dat-tiedostossa on 50 riviä. Ensimmäisessä sarakkeessa ovat 50 ensimmäistä ajanhetken arvoa t kahden desimaalin tarkkuudella. Toisessa sarakkeessa on taas seuraavat 50 arvoa jne. Viimeisessä 11. sarakkeessa on 28 arvoa, sillä data loppuu kesken. Tehtävä on oikein, kun output.dat-tiedosto näyttää seuraavalta:
Kolme ensimmäistä riviä
1.08 & 31.26 & 65.09 & 97.47 & 128.28 & 156.09 & 190.26 & 239.08 & 274.36 & 314.07 & 346.38 \\ 1.24 & 31.43 & 65.27 & 98.09 & 128.47 & 156.27 & 190.43 & 239.23 & 277.07 & 314.22 & 347.38 \\ 1.40 & 32.09 & 65.46 & 98.28 & 132.09 & 156.46 & 191.09 & 239.38 & 277.22 & 314.36 & 348.08 \\
Kolme viimeistä riviä
29.25 & 62.09 & 94.47 & 127.28 & 154.09 & 188.26 & 238.08 & 272.36 & 308.07 & 345.38 & \\ 29.43 & 62.27 & 97.09 & 127.47 & 154.28 & 188.43 & 238.23 & 274.07 & 308.22 & 346.08 & \\ 31.09 & 62.45 & 97.28 & 128.09 & 154.46 & 190.09 & 238.38 & 274.22 & 308.36 & 346.23 & \\Kiinnitä tässäkin tehtävässä erityistä huomiota tulosteen formaattiin. Nyt jokaiselle luvulle varattu tila on yhteensä yhdeksän merkkiä.